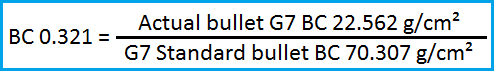Do Ballistic Coefficients have Units?

There are two definitions of ballistic coefficient in common use, one produces ballistic coefficients with units and the other produces ballistic coefficients without units. That would seem to create a contradiction until you realize that the units can be mathematically removed from ballistic coefficients, thus standardizing them across all systems of measurement. The need to standardize ballistic coefficients is self-evident given that, except for the United States, the industrialized world uses the Metric system.

Researchers use a definition that separates the shape of a bullet from its mass and diameter. The shape of the bullet is represented by the term "form factor" while the mass and diameter are represented by the term "sectional density." Ballistic coefficients calculated by this method have the same units as sectional density.

Industry, for the most part, defines ballistic coefficient as a ratio of the drag deceleration of an actual bullet as it relates to the drag deceleration of a standard bullet without treating shape and sectional density separately. This method, while once very difficult to do, is now readily done with modern instruments. For example, the Oehler Model 43 from 1992 calculated the ballistic coefficient for every shot fired in real time using the drag deceleration method without knowing anything about the bullet's shape. Ballistic coefficients calculated by this method have no units.

It's important to note that ballistic coefficients with units are equivalent to ballistic coefficients produced without units only when ballistic coefficients have the units of lb/in² (pounds per square inch). Converting such ballistic coefficients to g/cm² or kg/m² results in values that can't be used with most software, charts or graphs.

Drag Deceleration Method:

The drag deceleration definition of ballistic coefficient is the drag deceleration of the standard bullet divided by the drag deceleration of the actual bullet as shown in the following equation.

The units of deceleration, such as feet/sec² or meters/sec², cancel out and BC becomes a ratio that has no units, which is to say it's dimensionless. You can find this method defined in industry documentation such as in Sierra reloading manuals (2nd, 3rd, and 4th editions). Also, in his book Modern Practical Ballistics, Arthur Pejsa defines Ballistic coefficient as "Ratio of the retardation A of a projectile to that of a reference projectile." Retardation is just another term for drag deceleration.

Each standard projectile is designated by a "G" number, so if the G7 projectile is used then the ballistic coefficient is a G7 BC. It's easy to see from the equation that every standard projectile has a ballistic coefficient of 1.

Form Factor Method:

Form factor is a representation of a bullet's shape or form and is the ratio of an actual bullet's drag coefficient divided by a standard bullet's drag coefficient as shown in the following equation..

Drag coefficient is a dimensionless quantity as is form factor. Each standard projectile is designated by a "G" number, so if the drag coefficient is for the G7 projectile then the form factor is related to that same projectile. It's easy to see from the equation that every standard projectile has a form factor value of 1.

Ballistic coefficient is then defined by the following equation.

Which can be simplified into the following equation.

The resulting ballistic coefficient has the same units as sectional density, which are lb/in² for the English measurement system. For a standard bullet to have a BC of 1 it's sectional density must also be 1, and that only works out when using pounds for mass and inches for bullet diameter.

It might seem odd that the scientific definition depends on standard projectiles having a sectional density of 1 pound/inch², but this is the legacy of Francis Bashforth of England who was the first to propose using standard projectiles (circa 1870). Bashforth's proposed standard bullet had a weight of 1 pound and a diameter of 1 inch, which gives it a sectional density of 1.0 lb/in². Contrary to what many have been taught, the pound is the unit of mass in the Imperial Absolute system and the Poundal is the unit of force. That's also why lb-f/s (pound-feet/second) is the correct unit for bullet momentum.

As an example, given a bullet with a diameter of 0.338 inches and a mass of 300 grains the sectional density would be 0.375 lb/in² in the English system. If that bullet has a form factor of 1.169 relative to the G7 standard projectile then the example bullet would have a G7 BC of 0.321 lb/in². If using grams and centimeters in the metric system that same bullet's sectional density would be 26.375 g/cm² and it would have a G7 BC of 22.562 g/cm². Using kiligrams and meters would result in a sectional density of 263.747 kg/m² with a G7 BC of 225.618 kg/m².

No software designed for dimensionless ballistic coefficients or for ballistic coefficients in units of lb/in² would work with ballistic coefficients of 22.562 g/cm² or 225.618 kg/m². From a software developer's standpoint there needs to be a method of producing useful ballistic coefficients for users of the metric system. The following equation solves that problem.

Using values from the example bullet and plugging them into the equation for units in g/cm² gives the following.

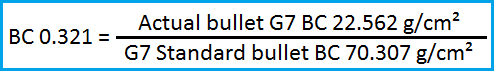
The resulting ballistic coefficient is the same as it was when in units of lb/in², and because the units cancel out, the value is now dimensionless just like the ballistic coefficients produced by the drag deceleration method. This simple step standardizes ballistic coefficient values across all systems of measurement, including the English system.

Being the ballistic coefficient value in lb/in² doesn't change when the units are mathematically removed, the obvious shortcut is to just drop the lb/in² units, which is not the same as ignoring them.

These dimensionless ballistic coefficient can't be plugged back into equations and used for research purposes without adding the units back, but other than that there seems to be no reason for retaining units for published ballistic coefficients. In fact, publishing ballistic coefficients with units of lb/in² creates confusion for users of the metric system, which is virtually everyone outside the United States. The burden of standardizing ballistic coefficients belongs to bullet and ammunition manufactures as well as software developers.